05. Calcolatori analogici

Il secolo della svolta per i primi veri calcolatori fu il 1600. Due furono le scoperte che maggiormente contribuirono al raggiungimento del calcolo automatico: (i) l'invenzione dei logaritmi e la scoperta delle loro proprietà aprirono la strada all'invenzione del regolo calcolatore; (ii) l'invenzione degli orologi (a pendolo) con il conseguente progresso della meccanica di precisione aprirono la strada alla costruzione delle prime calcolatrici meccaniche. Il regolo calcolatore e la calcolatrice meccanica, inventati quasi negli stessi anni, sono anche rappresentativi dei due paradigmi alternativi che hanno caratterizzato l'invenzione dei primi calcolatori: le macchine a rappresentazione analogica e le macchine a rappresentazione numerica (o digitale). La rappresentazione analogica si appoggia al concetto di grandezza fisica (ad esempio, la lunghezza) e rappresenta un numero come il risultato della misurazione di tale grandezza su un oggetto specifico (ad esempio, una certa asta). Nella rappresentazione numerica (o digitale), il numero viene rappresentato in modo discreto come un insieme composto da unità elementari considerate indivisibili (ad esempio, in una taglia ogni singola tacca, oppure in un abaco ogni singolo sassolino).

Tra i diversi tipi di calcolatori analogici quello che ha raggiunto la maggiore diffusione è stato certamente il regolo calcolatore. La strada per arrivare all’invenzione del regolo calcolatore fu aperta da Nepero agli inizi del 1600 con l’introduzione dei logaritmi, sebbene egli abbia utilizzato questa scoperta solo nell’ambito delle tavole matematiche.

Fig. 24. Regoli graduati con scale una doppia dell'altra: consentono di moltiplicare o dividere per 2. Una coppia di regoli dotati di opportune scale permette di effettuare diversi tipi di calcoli. In particolare, possiamo: (i) fare il raffronto di due scale vicine fisse; (ii) muovere un righello rispetto all'altro. Questi sono i meccanismi basilari per la costruzione di diversi strumenti analogici impiegati nel passato. L'esempio in figura illustra una coppia di regoli le cui scale sono una doppia dell’altra: in questo caso è possibile moltiplicare o dividere per 2 un dato numero. Questo principio è ancora oggi alla base degli scalimetri (descritti qui di seguito). Con una scala della funzione quadrato è possibile calcolare il quadrato di un numero oppure calcolare la funzione inversa radice quadrata. Il limite di questo approccio è quello di essere utilizzabile unicamente per funzioni matematiche ad un solo argomento. Si deve notare che il calcolo di una funzione (ad esempio, il quadrato di un numero) e della funzione inversa (ad esempio, la radice quadrata) comporta lo stesso grado di difficoltà.

Fig. 25. Regoli addizionatori. Utilizzando due scale metriche uguali incise su due righelli liberi di scorrere l'uno rispetto all'altro, è possibile realizzare un semplicissimo strumento per effettuare somme e sottrazioni. Ad esempio, dovendo sommare 6,0 con 5,5, si sposta il righello mobile in modo che lo zero della sua scala coincida con il valore 6,0 nella scala del righello fisso; quindi, sempre nella scala del righello mobile si cerca il valore 5,5; infine, il risultato della somma (cioè 11,5) può essere letto sulla scala del righello fisso in corrispondenza del numero 5,5. Con un metodo inverso a quello descritto è possibile effettuare l'operazione di differenza.

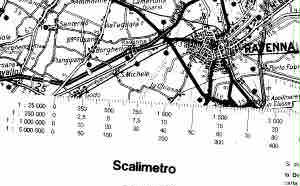
Fig. 26. Lo scalimetro è uno strumento particolare per la misurazione di distanze sulle cartine geografiche. Questo strumento permette di leggere direttamente le distanze reali sulla cartina evitando i calcoli necessari per la conversione di scala. Ogni scalimetro è di solito predisposto per lavorare con diversi rapporti di scala.

Fig. 27. Ricostruzione di un compasso di proporzione. Questo tipo di strumento veniva utilizzato soprattutto dai disegnatori che se ne servivano per ridurre o ingrandire i disegni secondo una data proporzione e ciò, in termini matematici, corrisponde alle operazioni di moltiplicazione e di divisione. Arricchendo lo strumento con altre scale era possibile suddividere i cerchi in un numero proporzionato di parti, determinare radici quadrate e cubiche, ecc. Nella figura, il perno è fissato sul valore 2: le aste a destra del perno hanno lunghezza doppia di quelle a sinistra del perno. Da ciò segue che ogni misura rilevata con le aste più lunghe risulta pari al doppio di quella indicata dalle aste più corte.

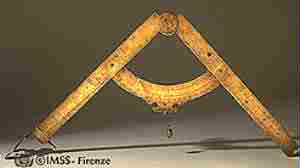
Fig. 28. Ricostruzione del "compasso geometrico et militare", realizzato da Galileo. I primi compassi geometrici (noti anche con il nome di compassi di proporzione) per il calcolo cominciarono ad apparire tra il 1500 e il 1600. In Italia uno dei primi ad introdurre questo tipo di strumento fu Galileo Galilei (1564-1642). Questo strumento, denominato da Galileo "compasso geometrico et militare", poteva essere impiegato anche in topografia, agrimensura e balistica grazie alle diverse scale dedicate a tali ambiti. Il principio di funzionamento su cui si basa questo dispositivo per eseguire moltiplicazioni e divisioni è simile a quello del compasso di proporzione e, in particolare, sfrutta le proporzionalità esistenti tra le lunghezze dei lati di triangoli simili.

Fig. 29. Compasso geometrico in avorio completo di tutti gli strumenti ausiliari, risalente al secolo scorso.

Fig. 30. Manuale d'uso originale (del 1649) del compasso di Galileo.

Fig. 31. Un nomogramma lineare per eseguire l’addizione. E' formato da tre scale lineari equidistanti. Con un righello si congiungono i due valori da sommare riportati sulle due scale esterne. Il punto in cui il righello taglia la scala intermedia fornisce la somma dei due numeri. Il principio di funzionamento di questo strumento è legato al concetto di punto medio: quando le tre scale sono equidistanti, il righello taglia sempre la scala intermedia nel punto medio m di due valori a, b scelti sulle scale esterne, ossia, in termini numerici, m = (a + b)/2. Se la scala centrale è doppia di quelle esterne, allora invece di fornire il valor medio di a e b, fornirà la somma a + b.

Fig. 32. Regolo calcolatore settecentesco in legno. Tra i diversi tipi di calcolatori analogici quello che ha raggiunto la maggiore diffusione è stato certamente il regolo calcolatore. Il primo regolo calcolatore in grado di eseguire moltiplicazioni e divisioni fu proposto dall'inglese Edmund Gunter (1581-1626) attorno al 1620 ed era basato su una scala logaritmica riportata sopra un regolo da utilizzare insieme ad un compasso. I primi regoli calcolatori erano di tipo circolare, mentre il primo regolo lineare simile a quelli attuali fu realizzato nel 1654 dall'inglese Robert Bissaker.

Fig. 33. Regoli moltiplicatori basati sulle potenze di 2. I due righelli moltiplicatori riportano le potenze di due: spostando un righello rispetto all'altro è possibile ricavare il prodotto di una coppia di potenze (di 2). Nella figura possiamo moltiplicare il numero 4 per un’altra potenza di 2. Il principio di funzionamento del regolo calcolatore è del tutto simile.

Fig. 34. Un esempio di prodotto (2,5 ´ 4,0) mediante il regolo calcolatore. Questo strumento, sfruttando le proprietà dei logaritmi e le capacità addizionatrici dei regoli scorrevoli, permette di svolgere rapidamente diverse operazioni facendo scorrere semplicemente il righello centrale o spostando un indice di riferimento.

Fig. 35. a. b. Due regoli calcolatori di forma diversa.

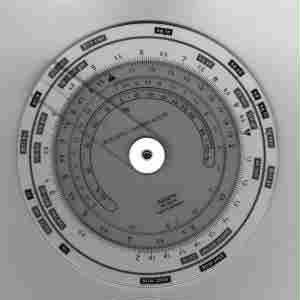
a. moderno regolo calcolatore circolare

b. regolo a disco per calcoli su strutture di cemento armato

Fig. 36. Curvimetro. Il curvimetro è uno strumento che permette di misurare la lunghezza di una curva tracciata su un foglio di carta. La misurazione viene effettuata seguendo il percorso della curva con una piccola ruota di scorrimento, la cui rotazione, attraverso una serie di ingranaggi, viene riportata da un’apposita lancetta su un quadrante con le varie scale. In termini matematici, per risolvere lo stesso problema sono necessari calcoli complessi che richiedono l’uso dell’integrale curvilineo.

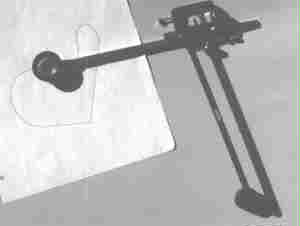
Fig. 37. Planimetro di tipo polare. Questo strumento costituisce l'analogo del curvimetro nella misurazione delle aree di figure (irregolari): seguendo il contorno della superficie da misurare mediante uno stilo si determina l'area della superficie. Il primo planimetro (di tipo ortogonale) sembra sia stato quello progettato da J.M. Herman nel 1814 e costruito poi nel 1817. Il planimetro polare, più preciso ed affidabile dei modelli precedenti, verrà inventato nel 1858 dal tedesco Amsler.

Fig. 38. Antico planimetro ortogonale per misurare superfici piane.

Fig. 39. a. b. Misurazione del volume di un solido mediante immersione in acqua. Un cilindro graduato permette di calcolare il volume di un solido per immersione in un dato liquido: la differenza tra il volume del liquido dopo l'immersione e prima dell'immersione rappresenta il volume del solido. Ovviamente, il metodo funziona con eguale semplicità con solidi sia di forma regolare che irregolare.

a.

b.

Copyright 1999-2001 Paolo Giangrandi - realizzazione web Tecnoteca s.r.l.